树状数组

算法

什么是树状数组?

它其实本质上和数组一样是一种数据结构，区别在于，它是树状的！（好像是废话）。

但是正是因为它是树状，所以它能高效的支持单点修改和区间查询！（并不是说它不能支持区间修改和单点查询。后面通过一些辅助数组和差分数组也可以实现）

树状数组具体能干什么？

如果你想知道一个数组1-7的前缀和，你会怎么做？

1
2
3
for(int i=1;i<=7;i++){
	sum+=a[i];
}

朴实无华的循环。时间复杂度O(n)

你也许会想，这还能玩出朵花来吗？当然，请相信代码世界有着无穷的创造力。

现在如果我告诉你，我知道a[1-4],a[5-6],a[7]呢？

那么当然就是这三个数的相加了。这就是树状数组的关键

我们总能将一段长n的区间拆成不多于logn段区间

接下来我将附上一张原理图，让你直观了解什么是树状。

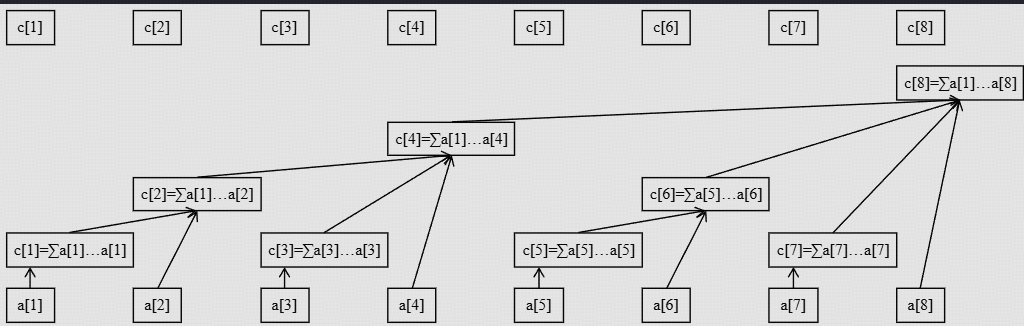
image-20250923200239382

image-20250923205827539

由图可知，减少时间复杂度的关键就在于c数组，那么问题来了

c[x]管辖的区间到底是什么？（lowbit引入预告）

树状数组中我们规定，c[x]管辖的区间是2的k次方（k是数的二进制表示中，最低位的1所在的位置）。

那么2的k次方就是x的二进制表示中最低位的1以及后面所有0组成的数字。

例如c88管辖哪个区间呢？它的二进制是01011000.那么它最低位的1以及后面的0组成的是1000，所以管辖八个元素。代表a[81-88]。对于1000，我们叫他，lowbit(88)。

代码如何实现lowbit(x)

这个就涉及到位运算知识了，补码反码的运算。这里不说原理了（犯懒）。

1
2
3
int lowbit(int x){
	 return x&-x
}

就是这么的朴实无华）

如何通过lowbit(x)实现区间查询

前面我们提到，树状数组可以实现区间查询有了lowbit之后，我们就可以轻松获得c[x]对应的a[]有几个，从而丝滑的实现区间查询了。

回顾上面提到的a[4–7]，

c7–lowbit(7)=1

c6–lowbit(6)=2

c4–lowbit(4)=4

令x不断地减去lowbit(x)直到等于0，就说明我们要找的数都找完了。

代码实现如下

1
2
3
4
5
6
7
8
int getsum(int x) {  // a[1]..a[x]的和
  int ans = 0;
  while (x > 0) {
    ans = ans + c[x];
    x = x - lowbit(x);
  }
  return ans;
}

如何通过lowbit(x)实现单点修改？

如果是a数组，那么单点修改不过是一个等于号的赋值操作。但是由于我们是通过c数组来计算以达到logn实现区间查询的目的，那么我们现在应该思考的问题是

如何通过修改c数组来单点修改a数组

不妨联想一下我们如何实现Sn->an
$$
Sn-Sn-1=an
$$
如果想要an +1，那我们只需要Sn +1.如果想要a(n-1) +1,那我们只要S(n-1)+1

(很简单的道理，1，2，3，4，5这个数组，我想要4变成6，那么S5 会变成17，S4会变成12，S3 是6不变。S4-S3=a4=6)

Cn其实也是另一种形式的Sn,只是他不是从1到n，但是他也是有规律的，这个规律就是lowbit(x)。

c[x]管理的区间是 [x - lowbit(x) + 1, x]

我们通过例子不难看出，本质上就是，谁包含我，我加上一个数，包含我的它也要加上一个数。

我们只需要通过lowbit向上搜寻，我们要加上的单点在哪个节点上即可。

以c[6]为例

  • c[6]管理 [5, 6]（lowbit(6)=2）
  • c[8(6+2)]管理 [1, 8]（lowbit(8)=8）
  • c[16(8+8)]管理 [1, 16]（因为 16 - 16 + 1 = 1）

(还可以往上延申

话不多说，献上代码！

1
2
3
4
5
6
void add(int x, int k) {
  while (x <= n) {  // 不能越界
    c[x] = c[x] + k;
    x = x + lowbit(x);
  }
}

来练练手叭（恭喜你已经学会了单点修改和区间查询）

image-20250924085013250

这是一道模板题，只要你理解了原理（不理解好像也没问题）就能丝滑的写出。#130. 树状数组 1 ：单点修改，区间查询 - 题目 - LibreOJ，附上题目链接，快去试试吧！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <bits/stdc++.h>
#define ll long long

using namespace std;
const int N = 1e6 + 5;
long long n, q, x, y, a, b, c[N];

int lowbit(int x) {
    return x & -x;
}

ll getSum(int x) {
    ll ans = 0;

    while (x > 0) {
        ans = ans + c[x];
        x = x - lowbit(x);
    }

    return ans;
}

void add(int x, int k) {
    while (x <= n) {
        c[x] = c[x] + k;
        x = x + lowbit(x);
    }
}

void solve() {
    cin >> y >> a >> b;

    if (y == 1) {
        add(a, b);
    } else {
        cout << getSum(b) - getSum(a - 1) << endl;
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    memset(c, 0, sizeof(c));
    cin >> n >> q;

    for (int i = 1; i <= n; i++) {
        cin >> x;
        add(i, x);
    }

    while (q--) {
        solve();
    }

    return 0;
}

如何实现区间修改，单点查询？

前面提到过，树状数组在辅助数组的帮助下可以实现区间修改。那么在我不提示的情况下，你不妨先思考几分钟，让子弹飞一会。

让我来猜一猜你现在是不是已经有了一个朴素的想法。

1
2
3
4
5
for(int i=l;i<=r;i++){
   int k;
   cin >>k;
   add(i,k);
}

但是这样，时间复杂度不是又上来了吗？那你何必费这么大功夫折腾树状数组（狗狗问号脸）

如果你现在一头雾水，毫无灵感这很正常，是因为你还没有遇见它–差分数组）

什么是差分数组呢？我们这里为什么会想到构造它？

不妨回顾一下我们前面我们是如何降低时间复杂度的。

其实就是构造一个关联的数组。那么除了树状拆分来得到c数组，我们其实还可以通过逆向求和的方式得到d数组也就是差分数组。

什么叫逆向求和?你可以通过an累加得到Sn，自然也可以通过Sn递减得到an.

Sn是an的求和数组，那么an也可以成为另一个人的求和数组。
$$
an-a(n-1)=dn
$$
这就是差分数组。其实听起来很简单吧。（事实上也很简单）

我们利用add方法来构造它

1
2
for (int i = 1; i <= n; i++)
        cin >> a[i], add(i, a[i] - a[i - 1]);

难的是，我们如何利用它把区间修改 转化成单点修改。

假设a数组 2 2 4 5 8 10

那么d数组 2 0 2 1 3 2

我现在想把a[2-3]加2，那么

a数组 2 4 6 5 8 10

d数组 2 2 2 -1 3 2

你动手算了一遍就会发现一个规律，其实我们区间修改[l-r]时，对于d数组来说，变的只有d[l]和d[r+1]。

这并不是什么神奇规律，这是差分数组的必然。a[l]作为第一个增大的元素，d数组只能依靠d[l]增长来让总和等于a[l]。而d[l]增大后x，意味着a[l]往后的数其实都会增大x。（就像a2增大2，那s2后面的数也都会增大2）.

问题来了，我们是要实现一个区间，而不是从一个数往后都增大。那其实也很简单。

在右界减去一个x不久好了？那么从r往后的数都会减去一个x。自然就实现了区间修改。

总结！

差分数组是一种常见的处理区间修改的技术：

  • 定义差分数组d，其中d[i] = a[i] - a[i-1]（a[0]=0）
  • 区间[l,r]加x的操作可以转化为：
    • d[l] += x
    • d[r+1] -= x

也许你会疑惑怎么就总结了，单点查询不是还没讲吗？有了d数组的情况下，我们如何求a?

这不就是朴实无华的 已知an求Sn吗。求个前缀和就好啦。
$$
a[i] = getsum(i) = d[1] + d[2] + … + d[i]
$$
也许你会疑惑，这时间复杂度不是又上来了吗？

看到求这个前缀和你有没有觉得熟悉呢，朋友。这不就是我们一开始引入树状数组要解决的问题吗？也就是前缀和查询功能。

那么再根据d数组构建一个属于它的树状数组tree，问题就迎刃而解了！

话不多说，奉上题目代码

[题目链接](#131. 树状数组 2 ：区间修改，单点查询 - 题目 - LibreOJ)

image-20250924095109141

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <bits/stdc++.h>
#define ll long long

using namespace std;
const int N = 1e6 + 5;
ll n, q, opt, x, l, r, tree[N], a[N];

int lowbit(int x) {
    return x & -x;
}

ll getsum(int x) {
    ll ans = 0;
    while (x > 0) {
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}

void add(int x, ll k) {
    while (x <= n) {
        tree[x] += k;
        x += lowbit(x);
    }
}

void solve() {
    cin >> opt;
    if(opt == 1) {
        cin >> l >> r >> x;
        add(l, x);
        if(r + 1 <= n) {  // 防止越界
            add(r + 1, -x);
        }
    }
    else {
        cin >> x;
        cout << getsum(x) << '\n';  
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    memset(tree, 0, sizeof(tree));  // 初始化tree数组
    
    cin >> n >> q;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        add(i, a[i] - (i == 1 ? 0 : a[i-1]));  // 更安全的差分初始化
    }

    while (q--) {
        solve();
    }

    return 0;
}

最后关卡，如何实现区间修改，区间查询？

恭喜你已经到了一维数组这一关的boss关卡，但我想说，这一关只和数学推导有关了。

区间修改我们无疑问的仍然使用差分数组，那么如何用差分数组实现区间查询呢？

原始数组a的前缀和可以表示为：
$$
sum[1..x] = Σ(i=1 to x) a[i]
$$
使用差分数组d（其中d[i] = a[i] - a[i-1]，a[0]=0）：
$$
sum[1..x] = Σ(i=1 to x) Σ(j=1 to i) d[j]
= Σ(j=1 to x) (x - j + 1) * d[j]
= (x+1) * Σ(j=1 to x) d[j] - Σ(j=1 to x) j * d[j]
$$
然后丝滑的
$$
sum[l..r] = sum[1..r] - sum[1..l-1]
$$
我们用两个树状数组维护sum[1-x]最后的两项结果即可
$$
(x+1) * Σ(j=1 to x) d[j] - Σ(j=1 to x) j * d[j]
$$
这正是我们使用两个树状数组维护的内容：

  • tree1维护Σd[j]
  • tree2维护Σj * d[j]

题目链接

附上AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll N = 1e6 + 5;
ll t1[N], t2[N];  // 两个树状数组

inline ll lowbit(ll x) {
    return x & (-x);
}

inline void add(ll t[], ll k, ll x) {
    for (ll i = k; i < N; i += lowbit(i)) {
        t[i] += x;
    }
}

inline ll sum(ll t[], ll x) {
    ll ans = 0;

    for (ll i = x; i > 0; i -= lowbit(i)) {
        ans += t[i];
    }

    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    ll n, m;
    cin >> n >> m;

    ll last = 0;

    for (int i = 1; i <= n; i++) {
        ll x;
        cin >> x;
        add(t1, i, x - last);
        add(t2, i, i * (x - last));
        last = x;
    }

    while (m--) {
        ll op;
        cin >> op;

        if (op == 1) {
            ll l, r, x;
            cin >> l >> r >> x;
            add(t1, l, x);
            add(t1, r + 1, -x);
            add(t2, l, l * x);
            add(t2, r + 1, -(r + 1) * x);
        } else {
            ll l, r;
            cin >> l >> r;
            ll prefix_r = (r + 1) * sum(t1, r) - sum(t2, r);
            ll prefix_l = l * sum(t1, l - 1) - sum(t2, l - 1);
            cout << prefix_r - prefix_l << "\n";
        }
    }

    return 0;
}

是的，到这里，区间修改，单点修改，区间查询，单点查询已经玩不起花了。

但是树状数组还没有结束！

因为这只是一维数组。树状数组还有plus版本，也就是二维数组。

欲知后事如何，请听下回分解~