本文将兼述数据结构这门课中链表的侧重点以及算法实战中链表的侧重点。
什么是链表？
链表是一种用于存储数据的数据结构，通过像链条一般的指针连接元素（得名原因）。它是线性表的链式存储映像，称为线性表的链式存储结构
它的显著优势是删除和插入数据十分方便（数组要O(n)，链表只需O(1)），但寻找和读取数据表现欠佳（数组只需O(1)，链表需要O(n)）。
链表的组成分类
链表由一系列节点（node）组成，每个节点（同结点）有两个部分：
- 数据域：存储实际数据，(如int value）
- 指针域： 存储下一个节点的地址（如 node *next）
链表分为，单链表，双链表，循环链表。
单链表
结点只有一个指针域，称为单链表或者线性链表。由表头唯一确定，所以可以用头指针的名字来命名。若头指针是L,则链表命名为L
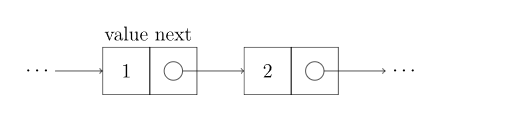
附上c++代码便于理解，但是后面会用到比较常见的typedef写法，所以这里的代码只是辅助理解，简洁为主。
注意：后文列举代码默认已定义Node结构体
1
2
3
4
5
| struct Node {
int value;
Node *next;
};
|
双链表
有两个指针域(有左右之分)的链表，称为双链表
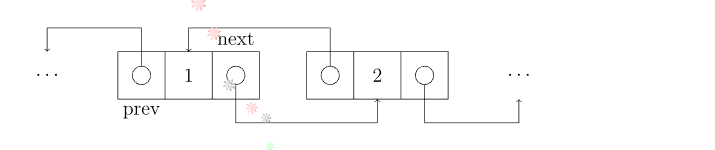
1
2
3
4
5
| struct Node {
int value;
Node *left;
Node *right;
};
|
循环链表
首尾相接的链表是循环列表。（尾节点的 next 指向头节点）由于这个特性，在插入数据时需要判断链表是否为空，为空则自身循环，不空则正常插入数据。（从循环链表中的任何一个节点都可以找到其他任何节点，而单链表不行）
1
2
3
4
5
6
7
8
9
10
11
12
| void insertNode(int i, Node *p) {
Node *node = new Node;
node->value = i;
node->next = NULL;
if (p == NULL) {
p = node;
node->next = node;
} else {
node->next = p->next;
p->next = node;
}
}
|
链表常见运算符和关键字
初见代码你也许疑惑，new是什么？
它是c++中的关键字，用于动态分配内存。
例如
1
2
| int *p=new int
int *p=new int (100)
|
->则是c/c++中的箭头运算符，等价于，先解引用指针，然后访问成员。
1
2
3
4
5
| int main(){
Node* node=new Node;
node->value=5;
node->next=NULL;
}
|
链表的一些概念
我们还提到了头结点的概念，其实与之对应的还有尾结点，头指针，首元结点。
- 头指针：指向链表中第一个元素的指针
- 首元结点：链表中存储第一个数据元素a1的结点
- 头结点：是在链表的首元结点之前附设的一个结点，**数据域内可以为空，**只存放表长和空表标志等信息。但此结点不能计入链表长度值
按有无头结点划分
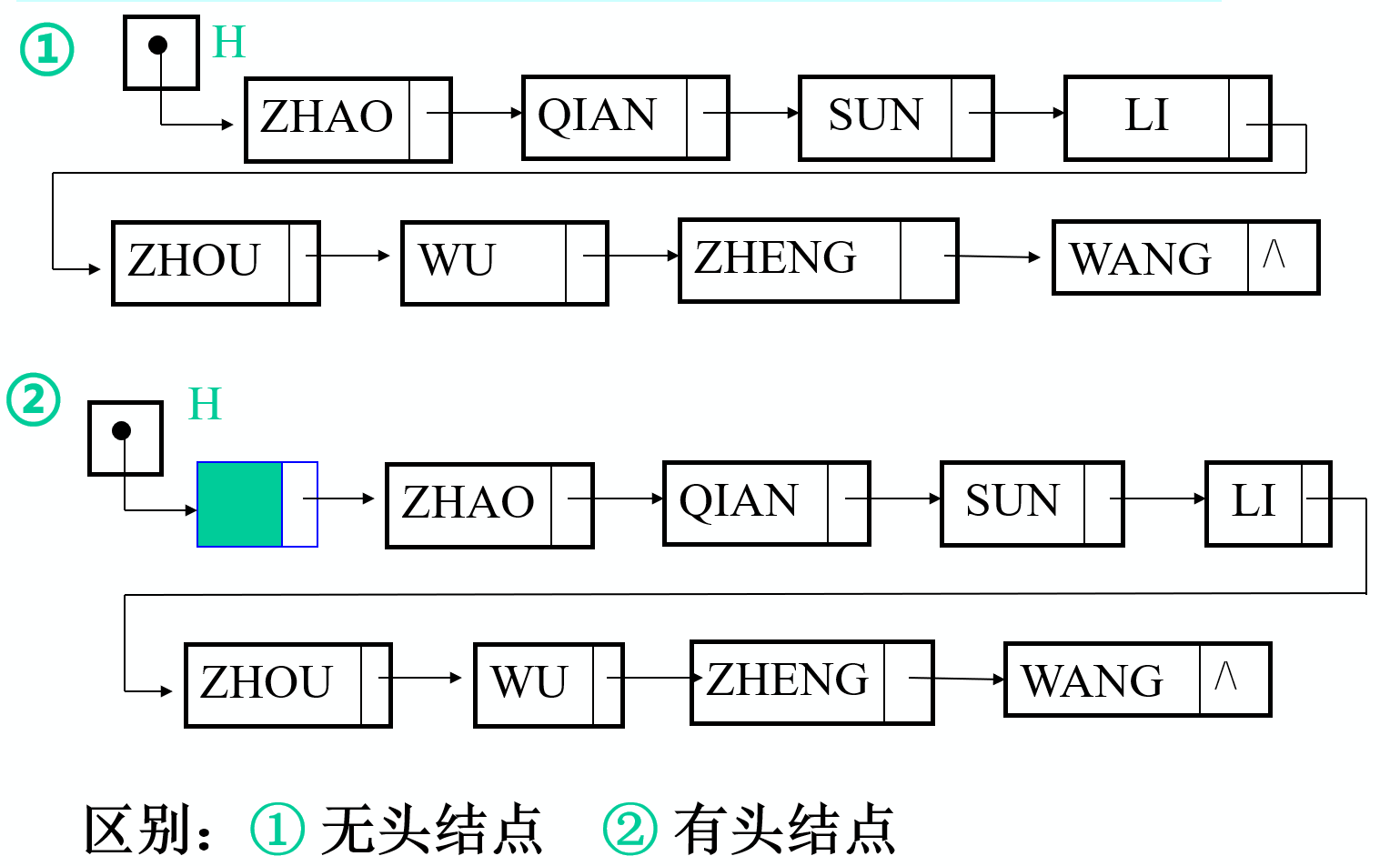
有头结点时，当当头结点的指针域为空时表示空表。
为什么要设置头结点？
链表的特点
这种存取元素的方法称为顺序存取法
单向链表的操作
- 初始化 2. 取值 3. 查找 4. 插入 5. 删除
初始化
注意，后文列举代码默认有此环境
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| #ifndef DULINKEDLIST_H
#define DULINKEDLIST_H
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef int ElemType;
typedef struct LNode{
int data;
struct LNode *next;
}LNode,*LinkList
|
取值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
int GetElem(LinkList L,int i,int *e){
LNode *p=L->next;
int j=1;
while(p && j<i){
p=p->next;
j++;
}
if(!p || j>i){
return 0;
}
*e=p->data;
return 1;
}
使用示例
LinkList list;
int value;
if(GetElem(list,3,&value)){
printf("第三个元素是：%d\n",value);
}
else{
printf("第三个元素不存在\n");
}
|
查找
1
2
3
4
5
6
7
8
9
10
11
12
|
LNode *LocateElem(LinkList L,int e){
LNode *p = L->next;
while(p!=NULL){
if(p->data==e){
return p;
}
p=p->next
}
return NULL
}
|
求表长
1
2
3
4
5
6
7
8
9
10
| int ListLength_L(LinkList L){
LinkList p;
p=L->next;
i=0;
while(p){
i++;
p=p->next;
}
return i;
}
|
判断是否为空
1
2
3
4
5
6
7
8
9
| int ListEmpty(LinkList L){
if(L->next){
return 0;
}
else{
return 1;
}
}
|
前插法建单链表
从一个空表开始重复读入数据
- 生成新结点
- 将读入数据放到新节点
- 将该新节点插入到链表
1
2
3
4
5
6
7
8
9
10
| void CreateList_F(LinkList &L,int n){
L=new LNode;
L->next=NULL;
for(int i=n;i>0;i--){
p=new LNode;
cin >>p->data;
p->next=L->next;
L->next=p;
}
}
|
尾插法建单链表
1
2
3
4
5
6
7
8
9
10
11
12
| void CreateList_L(LinkList &L,int n){
L=new LNode;
L->next=NULL;
r=L;
for(int i=0;i<n;i++){
p=new LNode;
cin >>p->data;
p->next=NULL;
r->next=p;
r=p;
}
}
|
插入（指定位置插入新节点）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
int ListInsert(LinkList L,int i,int e){
LNode *p=L;
int j=0;
while(p && j<i-1){
p=p->next;
j++;
}
if(!p || j>i-1){
return 0;
}
LNode *newNode = (LNode)malloc(sizeof(LNode));
newNode->data=e;
newNode->next=p->next;
p->next = newNode;
return 1;
}
|
删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
int ListDelete(LinkList L,int i,int *e){
LNode *p=L;
int j=0;
while(p->next && j<i-1){
p=p->next;
j++;
}
if(!(p->next) || j>i-1){
return 0;
}
LNode *q=p->next;
*e=q->data;
p->next=q->next;
free(q);
return 1;
}
|
[!NOTE]
关于p->next = q->next的绕过原理
假设一个链表 头节点-> A->B->C->NULL
p指向节点A,则p->next指向节点B，即q。
q->next指向c。
p->next=q->next就是直接让A指向C
单向循环链表的操作及约瑟夫环
初始化
1
2
3
4
5
6
7
8
9
10
11
|
#define OK 1
#define ERROR 0
#define OVERFLOW -1
typedef int Status;
Status InitList_CL(LinkList &L){
L=new LNode;
if(!L) exit(OVERLOW);
L->next=L;
return OK;
}
|
判断是否为空
1
2
3
4
| int ListEmpty_CL(LinkList L){
return (L->next==L);
}
|
结点p之前插入新结点s
1
2
3
4
5
6
7
8
9
10
11
| Status ListInsert_CL(LinkList &L,LNode *p,EleType e){
LNode *s=new LNode;
if(!s)return ERROR;
s->data=e;
s->next=p->next;
p->next=s;
return OK;
}
|
删除点p的后继节点
1
2
3
4
5
6
7
8
9
10
| Status ListDelete_CL(LinkList &L,LNode *p,EleType &e){
if(p->next==L)return ERRER;
LNode *q=p->next;
e=q->data;
p->next=q->next;
delete q;
return OK;
}
|
合并链表
Ta是链表a的尾指针，Ta->next指向链表a的头结点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| LinkList Connect(LinkList Ta,Linklist Tb){
p=Ta->next
Ta->next = Tb ->next->next;
delete Tb->next;
Tb->next=p;
return Tb;
}
|
约瑟夫环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| void Josephus(int n, int m) {
LinkList L, current, prev;
InitList_CL(L);
for(int i = 1; i <= n; i++) {
ListInsert_CL(L, i, i);
}
current = L->next;
prev = L;
while(n > 1) {
for(int count = 1; count < m; count++) {
prev = current;
current = current->next;
if(current == L) {
prev = current;
current = current->next;
}
}
printf("出列的人是：%d\n", current->data);
prev->next = current->next;
delete current;
current = prev->next;
n--;
if(current == L) {
current = current->next;
}
}
printf("最后剩下的人是：%d\n", current->data);
}
|
双向链表
定义初始化
1
2
3
4
5
6
| typedef struct DuLNode{
EleType data;
struct DuLNode *prior;
struct DuLNode *next;
}DuLNode,*DuLLinkList
|
插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
Status ListInsert_DuL(DuLinkList &L, int i, ElemType e) {
DuLNode *p;
if(!(p = GetElemP_DuL(L, i)))
return ERROR;
DuLNode *s = new DuLNode;
s->data = e;
s->prior = p->prior;
p->prior->next = s;
s->next = p;
p->prior = s;
return OK;
}
|
删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
Status ListDelete_DuL(DuLinkList &L, int i, ElemType &e) {
DuLNode *p;
if(!(p = GetElemP_DuL(L, i)))
return ERROR;
e = p->data;
p->prior->next = p->next;
p->next->prior = p->prior;
delete p;
return OK;
}
|
有序链表合并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
void MergeList_L(LinkList &La, LinkList &Lb, LinkList &Lc) {
pa = La->next;
pb = Lb->next;
pc = Lc = La;
while(pa && pb) {
if(pa->data <= pb->data) {
pc->next = pa;
pc = pa;
pa = pa->next;
}
else {
pc->next = pb;
pc = pb;
pb = pb->next;
}
}
pc->next = pa ? pa : pb;
delete Lb;
}
|